Never again: how a better understanding of aerodynamics and hydrodynamics could help prevent another Ever Given incident

Despite the industry's attempts to draw attention to the ongoing crew change crisis, the biggest shipping story of 2021 was undoubtedly the containership Ever Given becoming wedged across the Suez Canal. How can we stop such an incident happening in future? Captain Hamid Sarwar offers some instruction on the calculations needed to manoeuvre ships in canals and rivers

In the wake of the Ever Given incident in the Suez Canal earlier this year, it is perhaps prudent to highlight the issues and factors involved in navigating such waterways and to discuss how the manoeuvrability of a ship is affected while approaching shallower or narrower waters.

Ships are unique as compared with the other transportation industries like rail, road or air transport, in the sense that ships are moving in and are affected by two very different mediums: water and air.

Forces exerted on a ship by both of these fluids (air and water) are dependent on the speed of their movement and the exposed area of the ship. In other words, as a ship is partially submerged in the water and partially exposed to the air, we need to consider both the aerodynamics and hydrodynamics when it comes to discussing a ship's movement.

Aerodynamics and hydrodynamics

Force exerted by the air/water can be calculated by using the formulae, driven from the Kinetic Energy formula KE (Kinetic Energy) = ½ m v², as follows:

F = ½ x ρ x V² x A

where F = Drag force (Newtons)
ρ = Density of the medium (air/water)(Kg/m³)
V = Speed (Velocity) of wind/current
(m/Sec)
A = Area of ship exposed to wind/current
(m²)

From the above formula, we can appreciate that the Area of the ship exposed to the wind or current (water flow) is a critical value, along with the speed (velocity) of wind/current, in the calculation of the drag force.

Wind force will depend on the windage area of the hull above the waterline, and superstructure/deckhouses/deck cargoes etc. Current force will depend upon the wetted surface area of the hull underwater: all the areas below the water line.

It is the flow of air/water which exerts a force on the hull and all exposed areas of the ship; the flow can be measured using various instruments and then is available as real time values. These measured values can then be compared with the forecasted values to make a better navigational plan. Even the instruments onboard the ship can give a very good indication of the actual flow.

To get an idea of how much force is exerted on every square metre of the exposed area of the ship, and to compare between the wind force and the water force:

Assume a wind/current speed of 2.5m/s
(approx. 5 knots and typical values for air and water densities)
V = 2.5 m/s
ρ = Density of the air = 1.2 kg/m³
ρ = Density of the water (sea) = 1025 kg/m³

Air
F = ½ x ρ x V² x A
F = ½ x 1.2 x (2.5)² x 1
F ≈ 3.75 Newtons

Water
F = ½ x ρ x V² x A
F = ½ x 1025 x (2.5)² x 1
F ≈ 3200 Newtons

If the wind speed reaches 40 knots (20 m/s) then the force exerted will be:

Air
F = ½ x ρ x V² x A
F = ½ x 1.2 x (20)² x 1
F ≈ 240 Newtons

From this comparison it can easily be seen that water force is much greater than the air force due to the difference in the densities of the two mediums. Wind speed of about 30 knots (15m/s) exerts about the same pressure as 1 knot (0.5 m/s) of current.

A moving ship displaces the water equal to its underwater (submerged) volume, which in turns flows in all the different directions available, including flowing to the sides of the ship, providing the additional flow over the rudder and increased rudder efficiency but also creating a pressure force along the sides of the ship. So, because of the flow of water, a moving ship (let's say at 5 knots) can keep steerage for quite some distance even when the engine/propellers are stopped just by using the flow of water over the rudder, because of the forward motion of the ship. Distance travelled does of course depend on other factors e.g. propeller type, loaded/ballast condition and directional stability of the ship.

Where a ship is moving in shallow/confined waters, the water displaced may have very limited areas to go, and hence an increased flow may be experienced along the sides of the ship. This increased flow/velocity is the cause of three phenomena: 'bank effect', 'interaction' and 'squat'. The additional force exerted on the hull of the ship is the cause of reduced manoeuvrability of the ship in shallow/confined waters and has the potential to cause serious difficulties in steerage and course-keeping ability of the ship.

Mariners have experienced the effects of passing close to fixed or floating objects, and there has been guidance provided by different industry bodies on this subject area. Speed limits imposed within the approaches or passing a terminal are made for this very reason. Waterways like canals, rivers and dredged channels in the approaches to a harbour, with shallow waters around, present increased risk.

Focus on the Suez Canal

The blockage factor is the proportion of a midship's section of a ship/cross sectional area of the channel, river or canal.

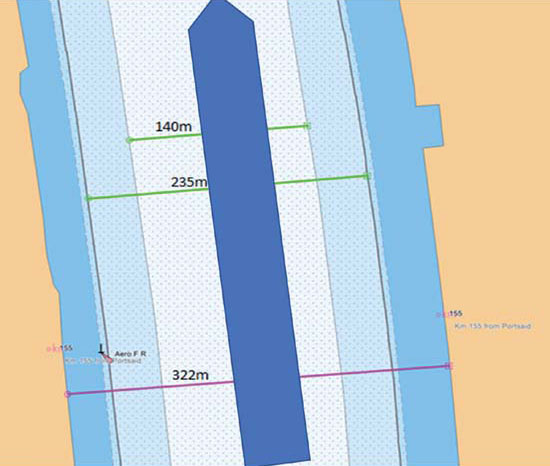
As we can see from fig. 1, a ship with similar dimensions can exhibit significant blockage factor.

This would mean that there would be a very limited space either side between the ship and the edge of the dredged channel for the flow of the displaced water. In fact, considering the dimensions of the dredged channel, it would not be much more than about 40m either side.

Water displaced by the above-mentioned ship:
Vol = 400 x 60 x 16 = 384000 m³

Assuming half of the water is moving ahead of the ship as bow wave and the other half is flowing either side of the ship i.e. 96000 m³ flowing either side of the ship, and also assuming a ship's speed of 13 knots, OR 13x1852=24076m/hour, which equates to about 401m/minute.

In other words, a 400m ship will travel its own length in about one minute. That implies a flow rate of 96000 m³/minute OR 1600 m³/sec

Focusing on the flow of water near the after end of the ship (i.e. rudder position) using the Flow rate formula Q = Av, where:

Q = refers to the liquid flow rate measured as
m³/sec - (1600 m³/sec)
A = refers to the area of the channel in
m²- (Dredged Area 25x40 = 1000m²)
v = refers to the velocity of the liquid in m/s
V = 1600/1000 = 1.6m/sec OR 5760m/hour,
which equates to about 3.1 knots

Going back to our hydrodynamics formula to work out the force exerted on every square metre:

Water
F = ½ x ρ x V² x A
F = ½ x 1025 x (1.6)² x 1
F ≈ 1312 Newtons

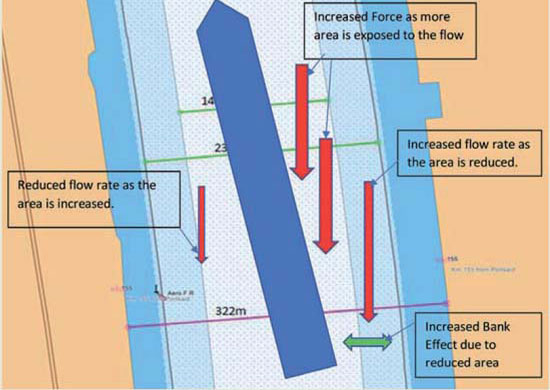
If the ship stems that flow precisely and manages to stay in the exact centre of the channel, then this flow does not cause any concern, but if the ship moves to one side of the channel or creates an angle with that flow (current) then there is an imbalance created which would result in an increased turning radius or reduced rudder efficiency.

That imbalance or angle can be created by the wind, as with the pivot point being forward, the ship would have a tendency to head into the wind or change course where the rudder was applied, and a little turning moment induced.

Conclusion

Increased flow of water around the hull of a ship can exert a significant force, and in turn affect the manoeuvrability of the ship. Turning circle, steerage and course keeping are the factors most affected. It can then become increasingly difficult to maintain a steady course as the ship experiences additional turning movements due to the flow of water and continuation of the imbalance between the port and starboard sides of the ship. This increased water flow is experienced whenever a ship moves from deeper and relatively open waters to confined waters.

In the above scenario, squat and its associated effects on manoeuvrability have not been considered, but we should note that a ship of similar dimensions and moving at similar speed in such waterways can easily experience a couple of metres of additional sinkage (squat), thus increasing the displaced water and the flow of water at either side. Squat can also reduce the steerage as the pivot point of the ship is changed.

Only by gaining a better understanding of all these factors and phenomena, to appreciate their effects on manoeuvrability of ships, can we be confident that never again will an incident of this type happen.

Nautilus member Captain Hamid Sarwar is a 'passionate' shiphandler who has over 15 years' shiphandling training experience.